I saw this on a vendor for about 120pp I am on a pvp server, untwinked, no alts to speak of. I was going to sell this for a profit, Its sure to raise mor emoney on a pvp but apparently its common nature might bring it way down on profit. Now, looking at it again I might just get it and use on my Ranger. He is almost 11, +20 HP and the mana not to mention raw ac is rather nice. Many people sell to the vendors but few buy from them. I have gotten items like arctic wyvern pelts for almost 100% profit and tomes of magic and so on.
``````
Got them for 120pp. Nice. Very nice. Anything that cheap that replaces my blackened alloy is way nice.
Edited, Wed Apr 7 16:22:06 2004

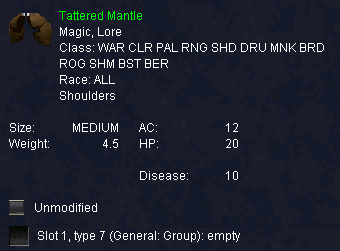
Tattered Mantle
|
[Drops | Comments ]
DropsThis item is found on creatures.Burning Woods
|
|||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
| Send a correction | ||||||||||||||||||||||||||||
#REDACTED,
Posted: Jan 04 2003 at 2:58 PM, Rating: Sub-Default, (Expand Post) i want to trade this item for crested spaulders on bertoxxulos becuase i plan on gettin a wurmy since they have been around 800 and one for 700 so i want to keep my stamina up.
Scholar
23 posts
This item is fairly common on Sol Ro and inexpensive (200pp or less). However, for a wood elf Ranger it is a must get early on. I obtained mine about level 8 and still have it at level 41. The reason is partly that it has good ac and nice benefits, but largely because anything better would cost thousands of pp (and it just isn't weak enough to make the top of my "to get list"). All of my other gear and weapons I have upgraded many times, but the ole tattered mantle is still a workhorse. It has given me more value for my pp then anything else I have acquired, and saved me a lot of dough in not having to upgrade repeatedly. I realize that many folks will dump on it (and me) because it is cheap and common, but I rate it 5 stars for overall value.
It seems to be fairly common drop. Killed it three times, dropped it three times last night. The people I was with thought that drop rate was typical.
I have been wearing crested spaulders up till now. Too bad I didnt know about the tattered mantle, although the crested isnt too bad. It has 11ac and +6 sta. I think another cheap item that one can consider to wear being a woodelf ranger ... although I am 43 now ... so I think i am travelling to the bazaar to check the prices here on Drinal on that mantle ....
added: they are usually for sale at around 400pp. I was able to buy mine though at 50pp. Be patience!
Edited, Sat Sep 28 11:38:06 2002
added: they are usually for sale at around 400pp. I was able to buy mine though at 50pp. Be patience!
Edited, Sat Sep 28 11:38:06 2002
#REDACTED,
Posted: Mar 01 2002 at 3:30 PM, Rating: Sub-Default, (Expand Post) i wode like to buy this ill be in rivervale tonight so if you wana trade be there name:hinuddar
19 posts
u are wrong bout the engraved grim pauldrons ;p go look it up
#REDACTED,
Posted: Jul 19 2001 at 10:12 AM, Rating: Sub-Default, (Expand Post) These are good for monks because they have good AC. You can deal with the weight if your other items are light. Sure beats Drovlarg Mantle. :)
Scholar
49 posts
You wear these for resist gear and decent AC, both of which come in handy against uber-type mobs that like to proc or cast disease-based spells (Severilous comes to mind).
Also, since Gullerback is the PH for the Wurmslayer wurm, there are a lot of these in circulation, making them a nice upgrade item in the path to hardcore gear (at least, that is, for people that aren't twinking to start).
Maladamuk Heartmender
Gnomish Cleric of the 48th Ring
Storm's Justice
Karana Server
Also, since Gullerback is the PH for the Wurmslayer wurm, there are a lot of these in circulation, making them a nice upgrade item in the path to hardcore gear (at least, that is, for people that aren't twinking to start).
Maladamuk Heartmender
Gnomish Cleric of the 48th Ring
Storm's Justice
Karana Server
I don't understand why a Warrior would choose these over a pair of Crafted Pauldrons. If you are a warrior, and have a good reason for wanting these, let me know. Maybe i want a pair and don't even know it yet.
V.
V.
12 posts
Crafted pauldron ac12 str2 wt 4.5
So you trade 2 strength for 20hp and 10RD
2str is almost but not completly irrelevant.
20 hp is arround a 1% increase in a warriors second important stat.
10RD is very nice in lots of hunting grounds.
IMO this is much easier to get and second only to granite spaulders.
So you trade 2 strength for 20hp and 10RD
2str is almost but not completly irrelevant.
20 hp is arround a 1% increase in a warriors second important stat.
10RD is very nice in lots of hunting grounds.
IMO this is much easier to get and second only to granite spaulders.
grim pauldrons would be second to granite spaulders to me ac 13 +10str i belive, could be wrong
Anonymous
This is much better than crested spaulders because 1) ac is 1 higher 2) HP is more most of the time, .1 hp per stam per level, so at level 40+, you'll get 24.. otherwise, u'll get less.. and even 4 hp is not worth 1 ac, since 1 ac at that level is multiplied.. AND you get 10 vs disease. There are your reasons.
Logan
Logan
I hope you realize that...
1) Not all Warriors have Crafted Pauldrons.
2) Other classes besides Warriors can wear this item.
1) Not all Warriors have Crafted Pauldrons.
2) Other classes besides Warriors can wear this item.
Alla has said it before, if the stats need to be corrected send him an email - dont post it because he wont see it
#Anonymous,
Posted: Dec 23 2000 at 6:44 PM, Rating: Sub-Default, (Expand Post) Allakhazam, you need to put monk down on these in the database. That was they'll show up in the searches.
#Anonymous,
Posted: Jan 10 2001 at 8:02 AM, Rating: Sub-Default, (Expand Post) at 4.5 lbs... no thanks I'll go nakid first
Free account required to post
You must log in or create an account to post messages.© 2024 Fanbyte LLC