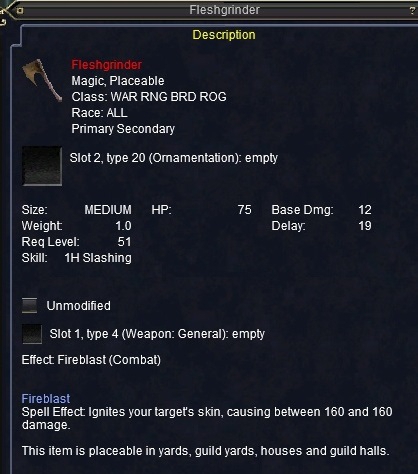
Fleshgrinder  

 

but gonne farm it anyway for my war hes gonne solo naggy! and vox ofcourse

I have a warrior and thought 2 would be better than one, and i was right...

Drop some of your strength and replace it with dexterity, you can easily keep aggro with 2 of these, and chances are you will do more damage from the procs than you will lose from dropping your strength, having a shaman in the group just makes it silly, in one easy test fight with 2 of these, with a dexterity of 230 (thank mr shaman) i got 23 procs off (3680 dmg) thats pretty awesome DPS may not seem much in the long run seeing as though most casters can do that in a few casts, but still any warriors with 2 of these will be a great warrior..

I just bought my second Fleshgrinder this weekend on Fennin Ro. I worked my way through level 58 this week in Plane of Disease so i had plenty of time to experiment with different combos. Like the earlier post, i had a Disembowler and a fleshgrinder at one point. While i did notice a drop in damage output (went from hitting for 70's to 60's) (always with max str) i noticed a huge increase in aggro. While a proc such as Frostbite on a frostbringer grabs the mobs attention faster then a grinder, it doesnt maintain it like the fleshgrinder does. Ive used both a fleshgrinder and frostbringer in primary and i can say that with 255 dex each time, the grinder procs a bit more than the frostbringer. Additionally, while it is true that the offhand weapon procs less often, i went from proccing on avg. 8 time a fight to a whopping 14 to 16 with 2 grinders (with 255 dex in both cases). Thats an additional 2240 to 2560 damage on top of my regular melee output which is quite high given the ratio of the fleshgrinders. Another thing to consider is resists. While the proc (fire based) is resisted every once in a while, when you are hunting in PoP against mobs that are avg level 55 (tier one mobs), your group will most likely have a slower (sham/enc) and they will be debuffing or tashing the mob anyway so 95% of the procs will hit. Prior to PoP, mobs in karnors castle or kael drakkal or whever you may be hunting simply do not have high resists due to the fact that they are are either cold based or level 50ish mobs.
Another thing that should be addressed in this post is all the warrior vs ranger crap. personally, i believe that pre PoP rangers were a fine main tank. now however, with the release of PoP, it has become very difficult for any class BUT a warrior to main tank in a group setting. This isnt because rangers are an inferior class, but rather due to the way VI has engineered the character classes. If a ranger had the hp/ac of a warrior, he wouldnt be a ranger, he'd be a warrior. Rangers werent programmed to have the kind of hps that warriors do and therefore cant handle the sort of damage that the PoP mobs dish out. On the other hand, i'd like to see a warrior shoot a mob with a bow for 1k+ damage. The classes are different and therefore have their own strengths and weaknesses (warriors included: lets see a warrior solo PoV/PoS/PoN etc)
Lastly, when it comes down to who should use the grinder, it reall doesnt matter. yes it generates aggro, but any good warrior will be able to maintain taunt over the mob no matter what his group does to it. 160 dmg from a proc is nothing compared to a sunstrike crit froma wizard. Just TAUNT.

Suurge Drackenfyre
59 warrior of Fennin Ro

For using a primary weapon would a FG be better or the Disemboweler? I've been pondering this for a long time. Disemboweler's are cheaper than a FG, but it does not have the proc. I've seen warriors and rangers say that they would prefer to go with a FG, but then from some I see them say it hardly ever procs. I know the +3 magic damage on the Disemboweler would be rarely calculated in on some of the higher end mobs. But is the FG's proc ever resisted?

Oriona Gladerunner
Warder

Edited, Thu Mar 6 11:29:40 2003

Um.. I am a 60 warlord. I would rather spank my monkey then argue over who is better a ranger or a Warrior.

Its as simple as this..
Warriors with alot of AA like myself suck damage up

Rangers do other stuff

I just picked up this weapon in the bazaar today (paid 60k btw) and am duel wielding it in my secondary slot with willsapper in my primary. I have found that I have a lot of difficulty getting this weapon to proc.

I know that offhand weapons proc less often than primarys but the proc rate is ridiculously low. My dex after the shammy buffs is over 230. I find that the willsapper procs about 6-8 times a fight, while the grinder MIGHT proc 1 fight in 10. While i was prmarily useing a JBoW before obtaining the grinder, I would often play around with other proc effects in the offhand. One of my favorites was SWoE, i found that this wepon, althgough with a much lower delay and less chances, would stil proc an average of one time a fight even in the offhand. Does anyone have similar results to this? Is it a slow procer?

I need the help of my fellow Warrior's. I am not interested in talking about the ability of a ranger to tank. Personally I play warriors so please all you would be tanks out dont flame or provide advice only real Warrior's. I am currently using a Fleshginder primary and a Frostbringer secondary. I have no problem holding taunt at all against all classes. ( well except the damn nukers that dont wait long enough lol). Ok to my question, I am interested in damage delt I hit anywhere from 35 to 60 in quads normally 3 sets of quads every 12 seconds mabe 4 . With occational crit for as much as 105. I do notice that my over all dmg is high but no where near most other classes is this normal or can I work in upgrade either equiptment or stat to gain more damage output?

hp unbuffed 2230
ac unbuffed 980
att unbuffed 950
str unbuffed 190
stm unbuffed 110
agli unbuffed 85


Dathgunz Champion 51'st season Prexus
Officer of The Legendary Dark Knights