There was a flirtation by SOE back in the EQ's hayday with a PVP server where each race spoke their own language and the "Good" races were at war with the "Evil" ones. There was no Common on said server. The Unknown Language is Human. The server shut down after not to long and was rolled into a regular PVP server with regular languages so "Human" was taken out of the game, that's why it shows as Unknown. People that obviously new the old Human language could teach it to others.
This language has no baring on the stats of the Heartstone as it came out during OOW which was way after that PVP server got shut down and the language removed.
Edited, Feb 19th 2023 10:12pm by hudge

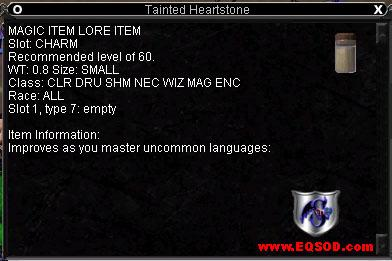
Tainted Heartstone
|
[Drops | Comments ]
DropsThis item is found on creatures.Wall of Slaughter
Item Lore: This stone is rimmed with dark knowledge Improves as you master uncommon languages. Shown with maxed stats. |
|||||||||||||||||||||||||||||
 Uploaded November 27th, 2008 |
||||||||||||||||||||||||||||||
| Send a correction | ||||||||||||||||||||||||||||||
1 post
I have this charm on a level 51 Cleric with maxxed out language skills and the recommended level of 60 now appears to be active. When I last looked at this charm several weeks ago, the recommended level was not active.
4 posts
You all are missing the point. It does not matter what languages you learn or in what order. This thing keys off of how many languages you have learned. You get skill increases for amount of languages learned not for what language was learned. Thus different people are seeing different increases on different languages.
Lady Turvey Jrai'Detbaen
Battle Cleric
Firiona Vie
Lady Turvey Jrai'Detbaen
Battle Cleric
Firiona Vie
1 post
I just maxed my tainted heartstone. I dont have the exact languages I learned in what order but I did notice that I didn't see any stat changes when I mastered goblin (the second to last one I learned), however when I maxed then next language and last for the uncommon languages (happened to be Elder Elvish) the stats increased by two steps i.e.: WIS went from 8 to 10. This may be why there is some confusion as to which languages raise the stats. If anyone trying this out could watch the 9th and 10th language they learn to see if this is repeated I am sure that others will appreciate it.
The uncommon languages seem to be any language that are not the language of a playable race, if you think of it that way it's easier to remember which ones you need. This does include ones like Dark Speech that some will know inherently but it isn't their race's language.
Kinlae
The uncommon languages seem to be any language that are not the language of a playable race, if you think of it that way it's easier to remember which ones you need. This does include ones like Dark Speech that some will know inherently but it isn't their race's language.
Kinlae
3 posts
OK .... I was able to max out all my lang. execept "kobold" at lvl 56 and got all the max beniffits listed .. so not sure why its recommended for lvl 60
11 posts
Anyone know if there is a meele version of this in which you improve it in the same way? Thanks!
30 posts
I have a 16 Druid that just finished mastering all languages and has the max stats already, no partial stats listed.
------------------
Skoter
70 Beastlord
Xegony Server
Edited, Thu May 18 08:19:13 2006
------------------
Skoter
70 Beastlord
Xegony Server
Edited, Thu May 18 08:19:13 2006
Interesting... I get max stats at level 42 - no partial stats displayed.
10/75/12 down the board.
10/75/12 down the board.
Jiriki Sa`Onserei, 120/67k AA Wood Elf Ranger
Anadriel Starfire, 120/46k AA High Elf Mage
Anadriel Starfire, 120/46k AA High Elf Mage
Scholar
26 posts
I just did this and wrote down the languages I learned on my Wizard in the order with the stats(Had no mastered languages)
Elder Tier'Dal - HP: +6 Mana: +6 End: +6
Elder Elvish - AC: +1 Cha: +1 Wis: +1 Int: +1 Agi: +1 Fire Resist: +1 Cold Resist: +1 Magic Resist: +1 HP: +12 Mana: +12 End: +12
Thieves Cant - AC: +2 Cha: +2 Wis: +2 Int: +2 Agi: +2 Fire Resist: +2 Cold Resist: +2 Magic Resist: +2 HP: +18 Mana: +18 End: +18
Goblin - AC: +3 Cha: +3 Wis: +3 Int: +3 Agi: +3 Fire Resist: +3 Cold Resist: +3 Magic Resist: +3 HP: +24 Mana: +24 End: +24
Gnoll - AC: +4 Cha: +4 Wis: +4 Int: +4 Agi: +4 Fire Resist: +4 Cold Resist: +4 Magic Resist: +4 HP: +30 Mana: +30 End: +30
Combine Tongue - AC: +4 Cha: +4 Wis: +4 Int: +4 Agi: +4 Fire Resist: +5 Cold Resist: +5 Magic Resist: +5 HP: +36 Mana: +36 End: +36
Orcish - AC: +5 Cha: +5 Wis: +5 Int: +5 Agi: +5 Fire Resist: +6 Cold Resist: +6 Magic Resist: +6 HP: +42 Mana: +42 End: +42
Faerie - AC: +6 Cha: +6 Wis: +6 Int: +6 Agi: +6 Fire Resist: +7 Cold Resist: +7 Magic Resist: +7 HP: +48 Mana: +48 End: +48
Dragon - AC: +7 Cha: +7 Wis: +7 Int: +7 Agi: +7 Fire Resist: +8 Cold Resist: +8 Magic Resist: +8 HP: +54 Mana: +54 End: +54
Elder Dragon - AC: +8 Cha: +8 Wis: +8 Int: +8 Agi: +8 Fire Resist: +9 Cold Resist: +9 Magic Resist: +9 HP: +60 Mana: +60 End: +60
Dark Speech - AC: +8 Cha: +8 Wis: +8 Int: +8 Agi: +8 Fire Resist: +10 Cold Resist: +10 Magic Resist: +10 HP: +66 Mana: +66 End: +66
Lizardman - No Change
Froglok - No Change
Old Erudian - AC: +10 Cha: +10 Wis: +10 Int: +10 Agi: +10 Fire Resist: +12 Cold Resist: +12 Magic Resist: +12 HP: +75 Mana: +75 End: +75
14 Languages in about an hour and a half, Better then my wooden figurine (No stats) Hope this helps.
Elder Tier'Dal - HP: +6 Mana: +6 End: +6
Elder Elvish - AC: +1 Cha: +1 Wis: +1 Int: +1 Agi: +1 Fire Resist: +1 Cold Resist: +1 Magic Resist: +1 HP: +12 Mana: +12 End: +12
Thieves Cant - AC: +2 Cha: +2 Wis: +2 Int: +2 Agi: +2 Fire Resist: +2 Cold Resist: +2 Magic Resist: +2 HP: +18 Mana: +18 End: +18
Goblin - AC: +3 Cha: +3 Wis: +3 Int: +3 Agi: +3 Fire Resist: +3 Cold Resist: +3 Magic Resist: +3 HP: +24 Mana: +24 End: +24
Gnoll - AC: +4 Cha: +4 Wis: +4 Int: +4 Agi: +4 Fire Resist: +4 Cold Resist: +4 Magic Resist: +4 HP: +30 Mana: +30 End: +30
Combine Tongue - AC: +4 Cha: +4 Wis: +4 Int: +4 Agi: +4 Fire Resist: +5 Cold Resist: +5 Magic Resist: +5 HP: +36 Mana: +36 End: +36
Orcish - AC: +5 Cha: +5 Wis: +5 Int: +5 Agi: +5 Fire Resist: +6 Cold Resist: +6 Magic Resist: +6 HP: +42 Mana: +42 End: +42
Faerie - AC: +6 Cha: +6 Wis: +6 Int: +6 Agi: +6 Fire Resist: +7 Cold Resist: +7 Magic Resist: +7 HP: +48 Mana: +48 End: +48
Dragon - AC: +7 Cha: +7 Wis: +7 Int: +7 Agi: +7 Fire Resist: +8 Cold Resist: +8 Magic Resist: +8 HP: +54 Mana: +54 End: +54
Elder Dragon - AC: +8 Cha: +8 Wis: +8 Int: +8 Agi: +8 Fire Resist: +9 Cold Resist: +9 Magic Resist: +9 HP: +60 Mana: +60 End: +60
Dark Speech - AC: +8 Cha: +8 Wis: +8 Int: +8 Agi: +8 Fire Resist: +10 Cold Resist: +10 Magic Resist: +10 HP: +66 Mana: +66 End: +66
Lizardman - No Change
Froglok - No Change
Old Erudian - AC: +10 Cha: +10 Wis: +10 Int: +10 Agi: +10 Fire Resist: +12 Cold Resist: +12 Magic Resist: +12 HP: +75 Mana: +75 End: +75
14 Languages in about an hour and a half, Better then my wooden figurine (No stats) Hope this helps.
Scholar
22 posts
Thank you for posting that! EXTREEMLY helpful!
Now THIS is the kind of forum post we need! Good work DragonBloods!
how do i get hotkeys to work with languages? i have my language set to elder dragon, but when i press my hotkey it says it in normal language.
figured it out. make sure if you use multiple chat windows to set all windows to the language you want to use.
5 posts
You only need to set language from the Main Chat window.
it says recommended level 60, that explains why stats are lower for some people
Wrong - rec levels don't affect charms.
worth 1350 tribute points
4 posts
well put new heartstone on toon that had previously learned all languages and stats went to max instantly.
Scholar
35 posts
If you are having trouble with getting your Heartstone to the max stats, try removing it and then replace it. I saw someone who had learned all the languages and was stuck at +8. He removed it and then replaced it and the stats went up to 10.
9 posts
I think it may also be level specific. My 56 chanter and 25 necro both have the same language skills. The level 25 has +7 stats, and the level 56 has +10 stats. The 25 languages are:
1. Common Tongue
2. Barbarian
3. Erudian
4. Elvish
5. Dark Elvish
6. Dwarvish
7. Troll
8. Ogre
9. Gnomish
10. Halfling
11. Thieves Cant
12. Old Erudian
13. Elder Elvish
14. Froglok
15. Goblin
16. Gnoll
17. Combine Tongue
18. Elder Tier'Dal
19. Lizardman
20. Orcish
21. Faerie
22. Dragon
23. Elder Dragon
24. Dark Speech
25. Vah Shir
Edited, Mon Nov 21 03:33:31 2005
1. Common Tongue
2. Barbarian
3. Erudian
4. Elvish
5. Dark Elvish
6. Dwarvish
7. Troll
8. Ogre
9. Gnomish
10. Halfling
11. Thieves Cant
12. Old Erudian
13. Elder Elvish
14. Froglok
15. Goblin
16. Gnoll
17. Combine Tongue
18. Elder Tier'Dal
19. Lizardman
20. Orcish
21. Faerie
22. Dragon
23. Elder Dragon
24. Dark Speech
25. Vah Shir
Edited, Mon Nov 21 03:33:31 2005
Gimly McGimly
Level 100 Dwarven Rogue
The Tribunal
Level 100 Dwarven Rogue
The Tribunal
ur missing language 26 "unknown language", i accidently found it. hint, it can only be learned from someone in a certain state.
22 posts
does anyone know what classes/race have thieves cant?? thank you
All Rogues--regardless of race--speak and can teach Thieves Cant.
My Chanter maxed it, learning it himself. He can speak it perfectly.
/chuckles
practically a year later.
my interpretation of thequestion was he wanted to know what class/race inherently spoke thieves cant, not what class/race could learn it; after all, learning a lang isn't restricted as you so usefully point out.
practically a year later.
my interpretation of thequestion was he wanted to know what class/race inherently spoke thieves cant, not what class/race could learn it; after all, learning a lang isn't restricted as you so usefully point out.
is my experience... just spent the evening working on 2 of my toons. neither had any points into any language, started with 1 language 100 and 1 at 50 (i don't count common). i did the 12 uncommon languages, and heartstone wasn't maxed... maxed out the language that was half done, and stone was done on both toons.
I saw this stone as a decent upgrade to the kobold charm that my three boxes had been carrying around for a year. I also had never done the language-thing before and was bored of AA grinding, so I bought two stones in the baz (one for 2k pp, the other for 1.5k pp) and started language skilling.
I began by making hotkeys for it. I made a marco button in the Socials page (in Actions) by typing "/gsay blah" (without the quotes) in all five lines. I then dragged a copy of the button to a Hotkey, then set that Hotkey to be pressed by an easily reachable keyboard key using the Options-Keys page (I chose the Numpad decimal key).
I then grouped my three boxes together, set each to speak their native language (in this case, barbarian, erudite and gnomish) and started tapping their hotkeys at a rate of about once per second. In about 10 mins, all three toons were skill 100 in all three languages. My erudite mage had previously skilled to 100 in froglok in a previous session and so I taught my other two toons that as well.
After this, I wondered how I would skill in those other languages without using up my precious training points. After playing around, I discovered what other posts have called "the ladder method" of language skilling. What it is, is that one toon can always teach language to another toon up to his own level plus one. For example, a toon at skill 5 can teach another toon to skill 6. Then the toon who was at 6 can teach the first toon to 7, who then teaches the other toon to 8, and so on until both are 100. Sweet.
For the next few hours, I skilled my toons. Here are things I noted as I progressed:
-the barbarian (a shaman) was consistantly slower to learn than the the erudite (mage) and gnome (sk). Since his wis is higher than the int of the gnome, the barbarian should have skilled faster. Based on this, I am convinced that only int (not the higher of int or wis) affects the skill rate of languages.
-the group window chats will say "tells the group in an unknown tongue..." until your language skill in that language reaches 25. After that, the chats will say "tells the group in goblin..." (or barabarian or whatever) and so identify what language is being spoken.
-Having 100 in barbarian, erudite, gnomish, froglok and old erudan did not increase the stone's stats.
-Sometime during the skilling of goblin (but before they reached 100), the stats went to +6 in hp, endurance and man.
-The stats at goblin 100 and faerie 2 was ac/cha/wis/int/agi +1, hp/end/mana +12, SV cold/fire/magic +1.
-At faerie 100, stats went to +2/+18.
-Skilling elder elvish did nothing.
-Skilling to gnoll +2 bumbed stats to +3/+24.
-Combine, dragon, elder dragon and dark elvish also increased all the stats.
-The rest of languages increased all or some of the stats...the languages were not consistant.
-After skilling my toons in all the languages they knew (each knew the same 23), ac/cha/wis/int/agi were +8, hp/mana/end were +60 and SV cold/fire/magic were +9. The languages they knew were:
Barbarian
Combine Tongue
Common Tongue
Dark Elvish
Dragon
Dwarvish
Elder Dragon
Elder Elvish
Elder TeirDal
Elvish
Erudian
Faerie
Froglok
Gnoll
Gnomish
Goblin
Halfling
Lizardman
Ogre
Old Erudian
Orcish
Troll
Vah Shir
Since the stone was not at the listed max, I looked at some posts here and at castersrealm and saw references to other languages. I found Thieves Cant on my rogue and after skilling my shaman in it, his stone hp/mana/end went up to +66 and the saves to +10.
I also found Dark Speech on my iksar and ogres and after skilling my shaman in it, his stone stats maxed.
There are references to a few other languages like Giant and Kobold and Dark Tongue, and that there are 26 languages, but I don't know where to find the other languages and don't know where to find this mysterious 26th language.
Good hunting,
Tamudan
BTW, each of my toons were over lvl 65 and started out with at least 1 point in every language.
Edited, Thu Oct 20 02:47:35 2005
I began by making hotkeys for it. I made a marco button in the Socials page (in Actions) by typing "/gsay blah" (without the quotes) in all five lines. I then dragged a copy of the button to a Hotkey, then set that Hotkey to be pressed by an easily reachable keyboard key using the Options-Keys page (I chose the Numpad decimal key).
I then grouped my three boxes together, set each to speak their native language (in this case, barbarian, erudite and gnomish) and started tapping their hotkeys at a rate of about once per second. In about 10 mins, all three toons were skill 100 in all three languages. My erudite mage had previously skilled to 100 in froglok in a previous session and so I taught my other two toons that as well.
After this, I wondered how I would skill in those other languages without using up my precious training points. After playing around, I discovered what other posts have called "the ladder method" of language skilling. What it is, is that one toon can always teach language to another toon up to his own level plus one. For example, a toon at skill 5 can teach another toon to skill 6. Then the toon who was at 6 can teach the first toon to 7, who then teaches the other toon to 8, and so on until both are 100. Sweet.
For the next few hours, I skilled my toons. Here are things I noted as I progressed:
-the barbarian (a shaman) was consistantly slower to learn than the the erudite (mage) and gnome (sk). Since his wis is higher than the int of the gnome, the barbarian should have skilled faster. Based on this, I am convinced that only int (not the higher of int or wis) affects the skill rate of languages.
-the group window chats will say "tells the group in an unknown tongue..." until your language skill in that language reaches 25. After that, the chats will say "tells the group in goblin..." (or barabarian or whatever) and so identify what language is being spoken.
-Having 100 in barbarian, erudite, gnomish, froglok and old erudan did not increase the stone's stats.
-Sometime during the skilling of goblin (but before they reached 100), the stats went to +6 in hp, endurance and man.
-The stats at goblin 100 and faerie 2 was ac/cha/wis/int/agi +1, hp/end/mana +12, SV cold/fire/magic +1.
-At faerie 100, stats went to +2/+18.
-Skilling elder elvish did nothing.
-Skilling to gnoll +2 bumbed stats to +3/+24.
-Combine, dragon, elder dragon and dark elvish also increased all the stats.
-The rest of languages increased all or some of the stats...the languages were not consistant.
-After skilling my toons in all the languages they knew (each knew the same 23), ac/cha/wis/int/agi were +8, hp/mana/end were +60 and SV cold/fire/magic were +9. The languages they knew were:
Barbarian
Combine Tongue
Common Tongue
Dark Elvish
Dragon
Dwarvish
Elder Dragon
Elder Elvish
Elder TeirDal
Elvish
Erudian
Faerie
Froglok
Gnoll
Gnomish
Goblin
Halfling
Lizardman
Ogre
Old Erudian
Orcish
Troll
Vah Shir
Since the stone was not at the listed max, I looked at some posts here and at castersrealm and saw references to other languages. I found Thieves Cant on my rogue and after skilling my shaman in it, his stone hp/mana/end went up to +66 and the saves to +10.
I also found Dark Speech on my iksar and ogres and after skilling my shaman in it, his stone stats maxed.
There are references to a few other languages like Giant and Kobold and Dark Tongue, and that there are 26 languages, but I don't know where to find the other languages and don't know where to find this mysterious 26th language.
Good hunting,
Tamudan
BTW, each of my toons were over lvl 65 and started out with at least 1 point in every language.
Edited, Thu Oct 20 02:47:35 2005
41 posts
Just verified that Old Erudian does indeed matter for the stats. Worked up the set for a friend and that was the missing link to max the stats at 10.
So the list is:
Thieves Cant
Elder Elvish
Goblin
Gnoll
Combine Tongue
Elder Teir'Dal
Orcish
Faerie
Dragon
Elder Dragon
Dark Speech
Old Erudian
Edited, Tue Oct 18 19:01:09 2005
So the list is:
Thieves Cant
Elder Elvish
Goblin
Gnoll
Combine Tongue
Elder Teir'Dal
Orcish
Faerie
Dragon
Elder Dragon
Dark Speech
Old Erudian
Edited, Tue Oct 18 19:01:09 2005
list is inacurate.
Goblin does not increase my charm stats.
So far Old erudin, thieve can't and elder elvish are accurate. HP is 24on mine after I maxed those language and after I learned goblin I still stuk at 24.
Goblin does not increase my charm stats.
So far Old erudin, thieve can't and elder elvish are accurate. HP is 24on mine after I maxed those language and after I learned goblin I still stuk at 24.
WRONG, goblin does increase stats. I just did it.
Did this today and can verify that this list is accurate. These are the ONLY languages you need to have maxed, and you DO need Old Erudian.
13 posts
My stats were at +8 I mastered Old Erudian and I got no increase. I then mastered Thieves Cant and it bumped it up to +10.
The languages I have at 100 are:
Thieves Cant
Elder Elvish
Goblin
Gnoll
Combine Tongue
Elder Teir'Dal
Orcish
Faerie
Dragon
Elder Dragon
Dark Speech
Ones that I have mastered but dont think affect it are:
Common Tongue
Dark Elvish
Lizardman
Old Erudian (positive this does not affect it)
Froglok
Can anyone verify which ones do increase the stats?
The languages I have at 100 are:
Thieves Cant
Elder Elvish
Goblin
Gnoll
Combine Tongue
Elder Teir'Dal
Orcish
Faerie
Dragon
Elder Dragon
Dark Speech
Ones that I have mastered but dont think affect it are:
Common Tongue
Dark Elvish
Lizardman
Old Erudian (positive this does not affect it)
Froglok
Can anyone verify which ones do increase the stats?
Irving Voxkiller 52 Cleric
Order of the White Dragon
Bristlebane Server
Order of the White Dragon
Bristlebane Server
13 posts
my stats on this charm are now maxed at what they say they should be.....the last lang i just found out about is dark speech, which is now maxed, as well as all of them. if u would like to learn this speech, if i am free on server EM feel free to look up syrendipity. i will teach it to u, also, u can teach urself ANY lang up to 32 in a group. hope this helps everyone out a little
13 posts
to my understanding, unknown language is when u are not high enough in the language to recognize it as a language. after u reach a certain point, it will tell u that they are speaking in that language. theives cant is a language that not many ppl have i have found out, but my husband had it trained at 1, so by using hot keys, we were both able to master this lang. in 15 min.
I maxed out all the uncommon languages and got max stats for my necro. I finished last night with all the uncommon languages and it said +8 stats and + 66 hp etc. then I logged back in tonight to finish the other languages and the stats were at maximum before I started. Apparently either the update this morning fixed it or just logging fixed it.
I also am not at level 60 but still have max stats.
I also am not at level 60 but still have max stats.
ok... there seems to be ALOT of confusion about mysterious *secret* languages and all... sooo heres the deal... there is none.. every single possible language WILL show up on the list when you go to a trainer for your class... you learn all those (not getting into the debate about which do and do not give powerups, just do em all)
my guesses for why peoples stats on their charms arent maxed are as follows:
#1.) they are not MASTER of all languages needed for max power (perhaps they look in their skills window and see all 100's, not realizing that a language with a skill of 0 will NOT show up even, go to a trainer and verify your languages)
#2.) perhaps they ARE master of all languages but are not lvl 60... look at the item.. recommended lvl 60.. if you are 59 you will not get full stats regardlessof how many languages you master
in short... go to your classes trainer... make SURE that all languages are done.. then make sure you're 60 and you'll have full stats... period
my guesses for why peoples stats on their charms arent maxed are as follows:
#1.) they are not MASTER of all languages needed for max power (perhaps they look in their skills window and see all 100's, not realizing that a language with a skill of 0 will NOT show up even, go to a trainer and verify your languages)
#2.) perhaps they ARE master of all languages but are not lvl 60... look at the item.. recommended lvl 60.. if you are 59 you will not get full stats regardlessof how many languages you master
in short... go to your classes trainer... make SURE that all languages are done.. then make sure you're 60 and you'll have full stats... period
Not necessarily correct. I had three toons at 65/66 that mastered all the languages given by their guildmasters and their stone stats were not maxed. I believe that there are some languages that trigger the stats and some that do not. So if the languages that your toon normally has includes all the triggers, then he needs no others. But if your toons do not normally learn these others due to race/class/deity, then the stone will not be maxed with only the languages found on their GMs.
You need all the rare languages, not just the ones the trainers offer. Certain races and classes have options that not everyone gets.
I just made sure that I had ALL 25 languages maxxed. I have full stats.
What I did, was found other prople who had one of these languages, and had them train me in it, while I offered another language in exchange.
I just made sure that I had ALL 25 languages maxxed. I have full stats.
What I did, was found other prople who had one of these languages, and had them train me in it, while I offered another language in exchange.
Quote:
my guesses for why peoples stats on their charms arent maxed are as follows:
No guesses needed. The item was bugged, and would not hit it's own max stats. Lucy showed it at +75 mana and hp, whereas the highest it would get was +72. My post just below quotes the developer who fixed it. The fix on test is now live.
BTW, I was level 70 when I got mine, and had every language maxxed. There is no secret language, nor was it a level or language problem. The item was bugged. It is now fixed.
Edited, Sat Aug 6 12:22:21 2005
OK. The ONLY reason I've ever seen for this item to not give correct stats, is that it is essentially one of the FIRST evolving items. You can either wait for the game to auto update it. You can Zone (any form of zoning counts). OR simplest of them ALL, is take it off, and put it back on. Which effectively forces it to update to YOUR character's CURRENT information.
Which is what I've done when skilling it up. Take it off, put it back on. When I finished each language, that's what I did. Took it off, put it back on. When the stats changed, I made note of the language. Tedious, annoying, and typical SoE coding. But, when you get right down to it, quite simple to work around.
When you zone, your character is polled from server memory, and just about everything about your character is recalculated everytime you zone. Its why you have sometimes less than max hp when you finish zoning, and your hp / mana tick up..... good rock solid SoE coding..... But, it doesn't effect SoE's end of gameplay, so, it is unlikely that it will ever be "fixed" unless someone fooks up and fixes it on accident......
Have a good one.
Which is what I've done when skilling it up. Take it off, put it back on. When I finished each language, that's what I did. Took it off, put it back on. When the stats changed, I made note of the language. Tedious, annoying, and typical SoE coding. But, when you get right down to it, quite simple to work around.
When you zone, your character is polled from server memory, and just about everything about your character is recalculated everytime you zone. Its why you have sometimes less than max hp when you finish zoning, and your hp / mana tick up..... good rock solid SoE coding..... But, it doesn't effect SoE's end of gameplay, so, it is unlikely that it will ever be "fixed" unless someone fooks up and fixes it on accident......
Have a good one.
5 posts
Just for everyone's Information there is a 26th Language and it is called Unknown Tongue. If u do not belive this come the The Nameless server. Make a crap alt and send Zuvus a /tell.Just tell me what it is about and i will come prove it to u.
This quote from an EQ designer on the eqlive forum linked below.
ANY language that you do not have above a certain skill in (fairly low, 20ish?), will cross your chat window as "soandso says, in an unknown tongue..."
Edited, Sat Jun 4 08:46:43 2005
Quote:
Sadly, it looks like this was merely some bad math. A secret language would've been much more exciting!
Anyway, I've fixed the script on Test. Both the Tainted Heartstone and Charm of Exotic Speech will work after the next patch.
Anyway, I've fixed the script on Test. Both the Tainted Heartstone and Charm of Exotic Speech will work after the next patch.
ANY language that you do not have above a certain skill in (fairly low, 20ish?), will cross your chat window as "soandso says, in an unknown tongue..."
Edited, Sat Jun 4 08:46:43 2005
There is a language that is called "an unknown tongue" that can be raised to 100 skill.
I have it as do several of my friends in game.
The language name is not capitalized as the others are and appears out of order at the bottom of the list of languages so I suspect it is a bug. I believe it is a placeholder from when another language was removed from the game and is not intended to be learned by PCs at this time.
The language is learnable through the usual method from someone who has it.
I have it as do several of my friends in game.
The language name is not capitalized as the others are and appears out of order at the bottom of the list of languages so I suspect it is a bug. I believe it is a placeholder from when another language was removed from the game and is not intended to be learned by PCs at this time.
The language is learnable through the usual method from someone who has it.
when you get a tell from someone saying <soandso> tells you, in an unknown tongue: <message here>
it just means they are speaking in a language you donnot know
Edited, Sat Aug 6 02:04:20 2005
it just means they are speaking in a language you donnot know
Edited, Sat Aug 6 02:04:20 2005
12 posts
While what you say IS true, there IS also a language that is labeled in the skill window as 'an unknown tongue'.
What they are saying is correct, I learned "an unknown language" on my shaman before I transfered from nameless to 7th, so I know for a fact that there is "an unknown language". I have it maxed, if ya want to know it keep an eye out for my shaman "Twistedbrujo" and if I have time I would be happy to teach it to you.
Edited, Fri Jan 6 19:02:00 2006
Edited, Fri Jan 6 19:02:00 2006
Mercy is for the weak, death is your redemtion, embrace me for I am Death!
I can confirm this, I was lucky enough to get a guildie from 7th Hammer who had 1 skill point in it, that's all it took. Now all guys on all four accounts are mastered in all 26* languages.
Any ideas of how to learn it if noone has it? I'm on stromm server.
- Vu~
Haven's Edge
Stromm
Haven's Edge
Stromm
Scholar
28 posts
contact my SK "Traine" on Stromm, i can teach you "an unknown tongue" to skill 100 nps
OK, just two minutes ago I finally maxed this thing on my chanter. You do need all 25 languages for it to be max. Started from ground zero today and learned the odd non-player races first. I rode at +8 stats until learning Barbarian (hardly an uncommon language) as my last language, now it is full up at +10/+75/+12 respectively. So the last requirement is likely to have all 25 max.
There is no Kobold or Giant Tongue anymore, so don't even worry about them. And to the person who said that other races can't max out the heartstone because the language isn't "uncommon" to them is just stupid. It just means they have one less language to master, gratz to them. Hurray...
AND THERE IS NO 26TH LANGUAGE. At least not as far as this item is concerned. I have heard of an unknown tongue, but in my experience it means that you speak it so bad you don't recognize it yet. Otherwise I have never heard of anybody learning "an unknown tongue", as though SOE couldn't come up with a name for a language, so just called it unknown. If it is there, it is a bug.
So have fun spammin the hell out of your groups, buddies, or whomever. If you are able to two box (or more), even better. Just group with yourself, chill in the guild hall, and go to town. Peace, I'm out!
There is no Kobold or Giant Tongue anymore, so don't even worry about them. And to the person who said that other races can't max out the heartstone because the language isn't "uncommon" to them is just stupid. It just means they have one less language to master, gratz to them. Hurray...
AND THERE IS NO 26TH LANGUAGE. At least not as far as this item is concerned. I have heard of an unknown tongue, but in my experience it means that you speak it so bad you don't recognize it yet. Otherwise I have never heard of anybody learning "an unknown tongue", as though SOE couldn't come up with a name for a language, so just called it unknown. If it is there, it is a bug.
So have fun spammin the hell out of your groups, buddies, or whomever. If you are able to two box (or more), even better. Just group with yourself, chill in the guild hall, and go to town. Peace, I'm out!
Free account required to post
You must log in or create an account to post messages.© 2024 Fanbyte LLC

