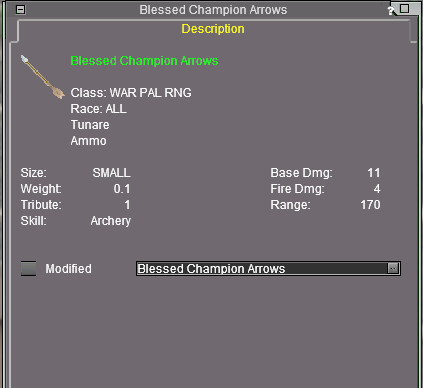
Blessed Champion Arrows
|
[Comments ]
Crafted: This item is crafted by players.
Yield: 1 x Blessed Champion Arrows See also: Blessed Guardian Arrows (Karana). |
|||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
| Send a correction | ||||||||||||||||||||||||||||
Sub combines, like mithril fletchings, now work.
I HAVE TRIED TO MAKE THESE AND THINK CONTAINER OR WHOLE RECIPE IS BUGGED I MA A WOOD ELF RANGER AS TUNARE AS MY DIETY AND DONE THE RECIPE TO THE BONE AND IT DOESNT NOT TAKE
Scholar
36 posts
I am a Wood Elf Tunare Ranger with 202 fletching skill and a fier'dal fletching kit, and I can't even get the sub-combine for the mithril fletchings to work. The forge sub-combines all worked fine, so I think the fier'dal fletching kit may be bugged.
No need to shout,man! Chill out!
You really shouldn't use all caps when you post. Many people are offended if you do.
Make sure you have the right ingredients(one of each) and your skill is high enough to do. I think some recipes require a specific skill level in order to do and these have a very high trivial(335). You may have to be a Grandmaster Fletcher to do it......but what do I know?..I have never fletched LOL :-)
Just seems logical to me.
You really shouldn't use all caps when you post. Many people are offended if you do.
Make sure you have the right ingredients(one of each) and your skill is high enough to do. I think some recipes require a specific skill level in order to do and these have a very high trivial(335). You may have to be a Grandmaster Fletcher to do it......but what do I know?..I have never fletched LOL :-)
Just seems logical to me.
I have a question about this. Since this lists a Slot Type 4, if you put an augmentation in here, assuming of course you have EQ, will the augmentation affect EVERY arrow you shoot? And then to go along with this, what would be the best augmentation to go in this slot??
If you check the raw data from Lucy, there is no augment slot.
is this the best damage arrow that there is? (forgetting that you may want to switch to different elemental versions)
No, this is not the best damage arrow there is. It was, once upon a time, but then Gates of Discord, Omens of War, Dragons of Norrath, and Depths of Darkhollow came out. This (and its cousin, the Blessed Guardian Arrow, which is Karana diety specific) is still the longest range arrow in the game.
The most damaging arrow is the CLASS 7 Drakebone Drakespike Arrow, which can be used by any bow-weilding class and race. These go for about 200pp EACH in the bazaar. Buy one. Save it until you get Endless Quiver.
The most damaging arrow is the CLASS 7 Drakebone Drakespike Arrow, which can be used by any bow-weilding class and race. These go for about 200pp EACH in the bazaar. Buy one. Save it until you get Endless Quiver.
Jiriki Sa`Onserei, 120/67k AA Wood Elf Ranger
Anadriel Starfire, 120/46k AA High Elf Mage
Anadriel Starfire, 120/46k AA High Elf Mage
10 posts
there is alot of debate out there how this modifier +4 fire works. i have heard it is best to use against stuff that fire spells can land for full on. i also heard just the opposite is true also, that this will do more damage against fire creatures. can someone give me some info on exactly how the mod works plz.
thanks
Herrox Stormchaser
thanks
Herrox Stormchaser
The fire damage, just same as a melee weapon with a damage, is calculated over the arrow's normal damage. Against a monster that has poor fire resist it adds that 4 damage, against a mob that has very high resist that damage will resist and you get the normal damage off arrow
8 posts
I Just what one thing what the recipe for these arrow if there crafted i going to start making them
3 posts
Goto eqtraders.com and look up cultural recipes in the recipes and look under wood elves section.It has everything there to make them.
#REDACTED,
Posted: Oct 30 2002 at 8:21 PM, Rating: Sub-Default, (Expand Post) If you can make these arrows on Ayonae Ro server, please send Impalanator a /tell.
Blessed Guardian Arrows, look em up
Thing about karana rangers is that we can go to PoG and kill everything there and still go back to our home city.
44 posts
Mine also carry a 4fire dmg as well.
Unfortunately Karanas HEF/HUM rangers got shafted when halflings was allowed to be rangers. halflings have best starting out stats of all races so tunare rangers have the table balanced out with equipment. In the endgame the tunare rangers have the advantage though since stats by that time are evened out. Perhaps when PoP comes out Karanas will remeber his rangers. If not just go kill him and take his loot. We Tunare rangers Love our god and I wont hunt her Plane out of respect =P. However I will gladly march into Karanas plane with my guild and kill him for ya. =D
Unfortunately Karanas HEF/HUM rangers got shafted when halflings was allowed to be rangers. halflings have best starting out stats of all races so tunare rangers have the table balanced out with equipment. In the endgame the tunare rangers have the advantage though since stats by that time are evened out. Perhaps when PoP comes out Karanas will remeber his rangers. If not just go kill him and take his loot. We Tunare rangers Love our god and I wont hunt her Plane out of respect =P. However I will gladly march into Karanas plane with my guild and kill him for ya. =D
there is an equivelent arrow for karana followers now. steel arrows. cant remember the name atm but they are the same stats as the tunare follower ones. but with cold damage instead of fire.
i know i am responding to an old post. but info is good.
they also have the bow equivelant to the tunare ones
Edited, Tue Dec 28 14:22:05 2004
i know i am responding to an old post. but info is good.
they also have the bow equivelant to the tunare ones
Edited, Tue Dec 28 14:22:05 2004
18 posts
Yet another wonderful ranger item that Karana ranger's can't touch just like those uber player made bows that about 1/3 of the rangers out there can't use
Get yourself a Nightmarewood Bow. No diety there, and it is the best non no drop bow in game IMHO. >=)
Yea when your 61 and get full use of the stats its a good bow
Hehe imagine a bug that would let you equip this in your primary or secondary hand, go get 2 of em and equip'em, things would die as soon as ya push attack with a 0 delay, that means no time between hitting which means you hit NON stop.
I read a while ago someone had found a way of doing just that - putting items in slots they weren't meant to go in. The method was to drop an item, position cursor so that it's over the dropped item, and over the slop you wish to place it. Then You were meant to click the item, and open inventory.
This was all before my time on eq, but i wonder if that means someone actually Did do this wil an arrow? You wouldn't even need a decent damage since the delay of 0 should mean everything dies in one? Although then there's minimum delays built into the game and yadda yadda yadda.
Nice idea though :)
This was all before my time on eq, but i wonder if that means someone actually Did do this wil an arrow? You wouldn't even need a decent damage since the delay of 0 should mean everything dies in one? Although then there's minimum delays built into the game and yadda yadda yadda.
Nice idea though :)
They fixed that bug sry.
5 posts
looked everywhere but havent seen any info on the recipe....intelligent responses will be greatly appreciated!!
25 posts
Welcome to the club of Karana worshippers getting the bad end of the deal...
The new zone on Test looks to have some higher end quests in it for Karana Rangers. My bet is actually that you will end up with better stuff in the end, due simply to VI's tendency to overcompensate wildly when they rebalance stuff like this. They should have implemented some Karana bows and arrows at the same time they did the rest, but when all is said and done I doubt highly that you will be having the same complaints when PoP comes out. Yes, they should redo it now, but Rangers have never been very high on the priority list for the Devs, and a subset of Rangers is probably even lower.
10 posts
SHD (Shadow Knight) is one of the usuable classes ?? How is this possible, you can not be a SHD and worship Tunare !
Is this item fake ?
Is this item fake ?
44 posts
the blessed champion arrows are deity imbued, but non imbued ones can be used by the classes. However seeing you post made me think. Perhaps theese can be made by changing the imbued componet to one of Innourk like the human cultral smithed armor can be imbued by many deities to include RZ, CT, EM, Inny, Karanas etc etc. perhaps thats why SHD are listed to cover all imbued versions of this arrows the stats be the same but deity will be differant.
Would you rather them leave classes OUT by accident?...
Pain Lord Darknyss Grimscale
92 Iksar Crusader of the Greenmist
92 Iksar Crusader of the Greenmist
The listed classes are Archery users, minus Rogues. Perhaps they meant to exclude ShadowKnights, but clicked the wrong item modifier. One of those "We'll fix it in the next patch" situations.
I started a halfling ranger cus I KNEW they would kick but !...
only problem is they CAN NOT worship Tunare.. =( ONLY karana boohoo
all these sweet arrows are tunare only ;( grrr
.
only problem is they CAN NOT worship Tunare.. =( ONLY karana boohoo
all these sweet arrows are tunare only ;( grrr
.
49 posts
15 total dmg asuuming no resists thats just nice...
The way they have archery working right now, its more like 11 Damage + up to 4 *points* of fire damage. Better than 11 Damage, but not hugely. However, the range on these is godlike. Get this and a Blessed Faydark Thunderbolt and you are effectively an over the horizon archer at 420 Range.
10 posts
Im pretty sure recommended lvl is the lvl you can use it,Or it is because you can max your trade skills at lvl 1. but gotta agree IT is so a monk item :P
#REDACTED,
Posted: Jun 12 2002 at 5:18 PM, Rating: Sub-Default, (Expand Post) Gotta love these new arrows, but I seriously think that Verant is smokin sumthin, a recommended lvl of 1; wtf?
5 posts
Yea give it to the monks, then along with all the other stuff they want they will be so over weight that they will have the agility and dexterity of Jobba the Hutt. Can't you just see them putting them monk moves on to a giant leach, I tremble in fear. A flying side kick from an 800 pound bowl of JELLO........Hey it might not kill you but you might die of indegestion as you ate your way out. Just hope those were carrots in there......
Edited, Wed Jun 12 20:06:12 2002
Edited, Wed Jun 12 20:06:12 2002
Free account required to post
You must log in or create an account to post messages.© 2024 Fanbyte LLC